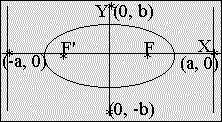
eccentricity < 1
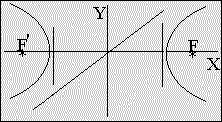
eccentricity > 1
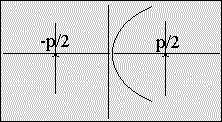
eccentricity = 1
An Overview of Geometries
[a work in progress, it's completed but has yet to be entirely transcribed into HTML]
Edited by Adrian Dorn
Consider:
The relation between 'x' and 'y' coordinates (x0,..., xn) and (y0,..., yn) of a specific point is given by the linear equations:
|
py i = S ai jxj (for j=0 to n) |
lxi = S bi jyj (for j=0 to n) |
| ai j, bi j : coefficients | p, l : proportionality factors |
Given an allowable coordinate system in Pn, a projective space, a set of homogeneous polynomial equations such as:
fi (x0,..., xn) = 0
Modern algebraic geometry is mainly concerned with properties of Varieties that are independent of the projective spaces in which the Varieties are embedded.
Much of classical algebraic geometry is devoted to the study of properties of Varieties invariant under bi-rational (U' Í U, V' Í V, U' <---> V') transformations.
A) The study of algebraic varieties is facillitated by means of local rings.
B) Irreducible subvarities of dimension zero <---> point.
C) A subvariety is considered a 'set'.
Considering A, B, and C, (from above) a variety 'U' is then a space 'X' consisting of points endowed with the Zarisky Topology with a ring associated with each 'point.' The set of rings is said to form a 'sheaf' over 'X'.
An algebraic variety can be represented as a ringed space.
The definition of sheaves can be extended to define sheaves of groups or other sets with an algebraic structure.
*The gist seems to be to regard algebraic varieties as ringed spaces and then studying the properties of sheaves over them.*
An affine variety considered as a ringed space is defined by an integral domain R(V, k), and the 'points' aredefined by the maximal prime ideals of R(V, k), where 'V' is the Variety and 'k' is the field. A polynomial 'vanishing' on a variety is a property of an ideal.
A sequence of sheaves and homomorphisms is referred to as 'exact' if the image of each homomorphism is the kernel of the following one [---> F1 ---> F2 ---> F3 --->....].
*Sounds like Chain Maps from Homology Theory.*
Other concepts:
A coherent sheaf over P (projective space) is just a finite-dimensional vector space over k (a field).
BOOKS:
The basis of analytic geometry is the idea that a point in space can be specified by numbers giving its position.
General equations for a line:
Also:
| | x y 1| | x1 y1 1| = 0 | x2 y2 1| 2 points |
| x1 y1 1| | x2 y2 1| = 0 | x3 y3 1| 3 points |
General Equation:
Ax² + Bx²y + Cxy² = Dx + Ey +F = 0
| Ellipse: | |
|---|---|
| x²/a² + y²/b² = 1 eccentricity < 1 |

|
| Hyperbola: | |
| x²/a² - y²/b² = 1 eccentricity > 1 |

|
| Parabola: | |
| y² = 2 · px eccentricity = 1 |

|
| *The parabola may be though of as a limiting case between an ellipse (e < 1) and a hyperbola (e > 1). It also may be considered as an elongated ellipse with its center, one focus and vertex all coinciding at infinity. The graph of a quadratic polynomial, y = ax² + bx + c, is also a parabola.* | |
Ax² + Bxy + Cy² + Dx + Ey + F = 0
(general equation for conic sections)
The coefficients, A, B, C, D, E, and F are completely determined by the eccentricity and the position(s) of the focus(foci) and directrix.
2) (B² - 4 · A · C) < 0
3) (B² - 4 · A · C) > 0
The 'radian' is the angle at the center of a circle that intercepts an arc equal in length to the radius:
The fundamental configuration to which the formulas of Spherical Trigonometry apply is the trihedral angle formed by 3 rays radiating from a point.
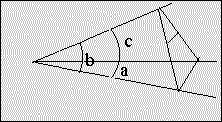
COS a = COS b · COS c + SIN b · SIN c · COS a
Area of a Spherical Triangle: A = E · r ²
| Polar Coordinates: (r, O) |
|---|
|
Linear Transformation: x = r · cos(O), y = r · sin(O)
The polar equation of a circle expresses the fact that |
|
Translation: x = x' + h, y = y' + h *A combination of dimensions describing a given system forces the centering of the highest degree components in terms of the whole system.* |
|
Rotation: x = x' · cos(O) - y · sin(O) y = x' · sin(O) + y' · cos(O) |
*They are homogeneous coordinates because for any 'k' not equal to 0, masses, kt 1, kt 2, and kt 3 have the same centroid as t 1, t 2 and t 3. These functions are rational.*
The extension of the Euclidean plane by postulating a line at infinity, the points of which lie on parallel lines called 'pencils', is a projective plane. In terms of Barycentric coordinates, the equation of the line at infinity restricts the {t k} to be: t 1 + t 2 + t 3 = 0.
General projective coordinates (x 1, x 2, x 3) are derived by the substitution t i = k i x i in which the coefficients k i are constants. The line at infinity can now be expresed as a linear combination of coordinates, k 1 x 1 + k 2 x 2 + k 3 x 3 = 0, and any other homogeneous linear equation represents an ordinary line. The transition to projective geometry is completed by waiving the distinction, so that a point at infinity is treated just like any other point. It enables the points of the projective plane to be defined as the ordered triads of numbers (x 1, x 2, x 3), not all zero, with the convention that (kx 1, kx 2, kx 3) is the same point for all 'k' not equal to zero.
The general homogeneous linear transformation: x i = S j c i j x j, in which the determinant (cij) is not equal to zero, transforms collinear points into collinear points, a collineation. For example: the collineation that leaves unchanged the first two coordinates and modifies the third with multiplication by a constant:
x'1 = x 1, y' 1 = y 1, z' 1 = kz 1
x'1 = x1, x'2 = x2, x'3 = x3,
Riemann Geometry: the geometry in a space of n-dimensions with the coordinates ua, a = 1,...,n, based on a quadratic differential form:
This geometry is of general form and includes as special cases the non-Euclidean geometries. It serves as a model of the physical Universe in Einstein's General Theory of Relativity.
Modern differential geometry stems from the basis that the objects of study are a class of spaces called *manifolds* equipped with additional structures. The main problems deal with the global properties that arise only when the manifolds are looked on as a whole. In global differential geometry, topology is a major tool.
A manifold is a space that is covered by a finite or a countable number of coordinate charts with each point in a chart described by the real coordinates x 1, ...,x n (called local coordinates), and such that when a point belongs to two charts and has two sets of local coordinates they are related by a transformation:
The Jacobian:
for:
{x i, x i j i,j = 1...n
{x 'i = f i (x 1,...,x n)
The determinant is non-singular, composed of continuous first partial derivatives (orthogonal). If a relation, F (f 1...f n) = 0 exists between the dependent variables, then J(f i/x i) = 0 and conversley, if the Jacobian equals zero, the f i's are related by at least one equation.
If all such functions f i have continuous partial derivatives of orders equal to or less than k, the manifold is said to be of class k. If all such functions have continuous partial derivatives of all orders, the manifold is said to be of class infinite. The local coordinates themselves have no geometric meaning, and the analytic tools for the study of manifold must be furnished by concepts that behave in a simple way under a transformation.
A tensor of contravariant order r and covariant order s is defined by specifiying its components in each coordinate chart. The tensor is called contravariant if s = 0, and covariant if r = 0.
A tensor of order one reduces to a vector. The vanishing of a tensor (i.e., of all components) is a condition invariant with a change of local coordinates.
All the tensors of given orders at a point form a vector space and the collection of all of them forms a tensor bundle of the manifold M.
All the contravariant vectors form a tangent bundle of M; covariant, cotangent.
The tensor bundles are special cases of a general vector bundle over M. A vector bundle over M is a collection of vector spaces over the points of M such that it is locally a product and that the linear structures on the vector spaces (fibres) have a respective representation.
Together with "virtual bundles" (negative numbers in arithmetic) all the finite linear combinations of the vector bundles over M are made into a group. Through the tensor product of vector bundles the group acquires a multiplication and has a ring structure called the Grothendrisk Ring, a significant global invariant over M.
The space of all frames at a point P of M is a fibre and is called the principal fibre space; its dimension is n 2 + n.
A real-valued function is a tensor field of order zero, and its partial derivatives are the components of a covariant vector field called the gradient.
Exterior differential forms are the integrals of multiple integrals.
If D is the boundary of an (r+1) dimensional domain F, then the integral of w (an arbitrary quantity) over domain D is equal to the integral of dw over domain F.
Another important operation for tensor fields is the Lie derivative:
X f = S A k (d/d(x k) f
A vector field X defines an infinitesimal transformation which leads to a new tensor field of the same type:
d x i = A i dt, i = 1,...,n
A Riemannian manifold has a uniquely determined connection, the Levi-Civita connection which is characterized by:
In the special case of the affine space where the connection is defined by T ji k = 0, parallelism of A j k means the constancy of all the components.
An exterior differntial form is called closed if its extrerior derivative is zero; it's called a derived form if it is the exterior derivative of another.
Two closed forms belong to the same class iff (if and only if) their difference is a derived form.
*A manifold is compact if it can be covered by a finite number of coordinate charts.
All the classes of closed forms of degree # form a real vector space. This space is manageable in the sense that contrast exists to the space of all forms of degree # or even that of all closed forms, both of which are infinitely dimensional.
The dimension of a compact manifold represented by the above described space is the #th Betti number of the manifold. The Betti number is an integer and is a topological invariant of the manifold that describes its connective properties.
Aside: What does closure have to do with homogeneity?
A form is called harmonic if it is both closed and co-closed.
On a compact orientable Riemannian manifold there is exactly one harmonic form in every class of closed forms of degree #.
If an exterior differential form is independent of the choice of the local chart, then the group of form classes are defined over the whole manifold, and are closed.
Pontryagin Characteristic (k, even):
A fundamental theorem on characteristic classes postulates that for odd k, Pk is a derived form, whereas for even k, Pk determines a class.