Of all quadrilateral prisms with a given volume, the cube has the least surface area. A cube is defined as a regular quadrilateral prism.

By using the reflection principle we are able to increase the area of an irregular figure without increasing its perimeter.

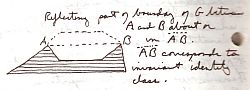The above three assertions are from what is called The Isoperimetric Theorem. It's a simple theorem with profound implications. To whit: Sometimes we can widen the class of allowed figures and thereby solve a problem for which no extremal figure existed previously, and sometimes by restricting the class of figures we can do the same. Isoperimetric theorems stress the importance of principles of symmetry and reflection of dual concepts. Reflection about a line formed by two points on either side of an empty area of an irregular figure [a piece missing] expands the area without increasing the perimeter. Reflections are maps.

All mathematical processes can be characterized in terms of maps. For example, the polynomial equation--ax² + bx = 0--is the basic question that maps to its set of solutions or roots. Any set of questions which renders the same answer must be the same question--multiples. Therefore, this basic equation, or invariant vector, is a particular aspect of a mathematical system seen as a component of symmetry; the fundamental equation of the equivalence class generates the system, and so acts as one of its mechanisms.

Algebraic analysis answers questions and seeks information about form and structure, general principles or invariants, by eliminating redundancies and testing for common ground, fine-tuning characterizations. Every algebraic structure has at least group symmetry. Galois demonstrated that, in general, the quintic (fifth degree polynomial) is not solvable by ordinary means. There is no fifth degree symmetry; the splitting of conjugates (the roots of the equation) is not complete. There are, of course, many exceptions to this rule; however, we are not interested in those.

The symmetry group, S₅, containing five factorial (120) elements is the group of permutations on the roots of the quintic. In order for a group of permutations on the roots of an equation to be solvable and the associated equation reducible, each factor group of its composition series must be simple (invariant and nondivisible) and abelian. The quintic series is {E, A₅, S₅}. A₅ is the smallest non-abelian simple group and is referred to as the alternating group, the group of even permutations. Additionally, the factor group, A₅/E, is isomorphic to A₅ and is therefore also non-abelian simple [An isomorphic map preserves invariant, geometry-defining features in one-to-one correspondence. (Felix Klein)]. That's the basic theory.

From another perspective, in the case of the quintic, on the fourth dimension we have an autonomous component. What does this mean? The central axis of reflection has no inverse element throughout; only if each factor representing the quintic were abelian (commutative) would that be the case. Imagine these factors as solid objects composing a structure with a center of gravity. The first three dimensions would balance, but on the fourth we have an asymmetrical extension jutting away from the main axis necessitating a counterbalance. Thus there is no single generator of the whole group. Or, there is no 5th degree symmetry of the type with only one central axis. So, we have an asymmetric configuration for which we need an imaginary reflection.

The Complex Field is a two-generator [related] form of symmetry. While the real part generates the asymmetric component, the imaginary part generates the opposite or reflective component [or should I say: 'reflective asymmetry aspect'], and by so doing imposes symmetry.

It is not a function if it does not define. The definition of a function is that of the definer. An equation defines an equivalence relation on a set of elements, say, numbers. The Identity equivalence class of the quintic is undefinable without relabeling all roots against the background of the two-generator symmetry system--the complex numbers. Considering the irreducible polynomial for which there is no defined Identity equivalence class over the field to which it is restricted, in order to reduce it (solve it) we must relabel to make the environment compatible for the prime factor. In actuality, we are applying more restrictions to our base field by dictating the form each number must take. We thereby garnish more information by taking this peculiar point-of-view of the irreducible. Phase shifting or twisting compared to hyperscaling. It increases the fundamental unit by one full dimension while still allowing for supersymmetry. [The Complex field is actually a higher-ordered symmetry, not just the result of adding one independent vector to the Reals.]

1) Reducible polynomial has axis of symmetry bisecting root segment, roots acting as end points or conjugates.

2) Non-reducible polynomial needs phase mapping: b maps to b(irr)

Like a planar projection, in order to align reflection symmetry plane. You have no group without reflection symmetry for each element.

3) In Complex space: Each Real number is composed of two complex conjugates. Imaginary symmetry is an increased gradation of magnification, and therefore reveals the Complex number field within the Real number field [as in: atoms, nucleons, quarks]. Therefore, any Real number solution to a polynomial, reducible or nonreducible, has a conjugate. All complex solutions, or roots, come in pairs.

A number--A--in the Real realm can be written as A + 0i in the Complex. But...

Caveat: When two different forms are said to be equivalent, it does not mean they are equal, that one could be replaced by the other, but rather that they each represent the same aspect or position in the overall symmetry of quite different, yet isomorphic, realities.