 The idea of a simplex is easy to visualize. For example, a 2-simplex can be thought of as a closed triangle with three vertices and three line segments--or edges--acting as its boundaries connecting the vertices. But, topologically, it can take any cell-shape, a cell being a generalization of a simplex. Each 2-dimensional cell is homeomorphic--maps invariants to invariants--to the Euclidean space R2. Topologically, an n-simplex is equivalent to an n-ball.
The idea of a simplex is easy to visualize. For example, a 2-simplex can be thought of as a closed triangle with three vertices and three line segments--or edges--acting as its boundaries connecting the vertices. But, topologically, it can take any cell-shape, a cell being a generalization of a simplex. Each 2-dimensional cell is homeomorphic--maps invariants to invariants--to the Euclidean space R2. Topologically, an n-simplex is equivalent to an n-ball.
Convention states that points on the boundaries of a surface do not have neighborhoods. The space must be open, in other words, for all points to have neighborhoods. Why? Visualize a 'point' on the boundary of a figure or an end 'point' of an interval. And also visualize a 'nbhd' as completely encapsulating, enclosing, enfolding that point as a cocoon would. A point on the extreme outer edge, beyond which there is nothing, no space, not even infinitesimal, cannot be contained within the interior of a nbhd.
However, according to an article in Wikipedia: "Every boundary point has a neighborhood homeomorphic to the "half" n-ball." It hinges on treating the interior and the boundary as separate manifolds: "If M is a manifold with boundary of dimension n, then Int M is a manifold (without boundary) of dimension n and ∂M is a manifold (without boundary) of dimension n-1." So what you end up with is a union of manifolds instead of one continuous surface. In much the same way, a closed simplex can be considered as the union of its interior and the boundary.
 Now, the significance of a manifold lies in the fact that compared to a polyhedron, it is all of one piece, a continuum. That is to say, it has no sub-partitions joined together as does a polyhedron with its polygonal faces. Each point/neighborhood of a manifold corresponds to a local flat Euclidean plane; so, in a sense, considering that a manifold is composed of points, it can be said to be Euclidean-ized.
Now, the significance of a manifold lies in the fact that compared to a polyhedron, it is all of one piece, a continuum. That is to say, it has no sub-partitions joined together as does a polyhedron with its polygonal faces. Each point/neighborhood of a manifold corresponds to a local flat Euclidean plane; so, in a sense, considering that a manifold is composed of points, it can be said to be Euclidean-ized.
In brief, a (real) n-dimensional manifold is a topological space M for which every point x ∈ M has a neighborhood homeomorphic to Euclidean space Rn. From Wikipedia, we have: "A simplicial manifold is a simplicial complex for which the geometric realization is homeomorphic to a topological manifold."
So we have: closed simplex equals cell equals manifold. By the use of barycentric coordinates we can further sub-divide the cell into simple quotient spaces to create a polyhedron of space. With each factoring we create a composition series, further refining the cell's detail. The cell, it may be pointed out, is susceptible to continuous deformations. In the process, its interior morphology rearranges its play of symmetries in a dynamic and self-organizing manner. And as the interior of a cell is sensivitve to its boundary shape, it is said to be shape-aware, analogous in regulatory capacity or methodology to the morphogenetic field of a biological cell. An important point that shouldn't be underestimated concerns the orientation -- spin -- imposed on a simplex, infusing it with a causal asymmetric tendency effecting ripples and contours. This feature eliminates random inconsistencies.
-
→ Click image to the right for larger version
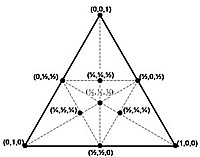 A change of basis takes place; we zoom in. Barycentric coordinates expand the vertices onto a smaller, more refined scale, adding degrees of freedom, revealing underlying dimensions. As the space grows in complexity, each vertex, boundary and interior point transforms into a linear combination -- weighted by the barycentric coordinates acting as coefficients -- of the newly defined vertices. Essentially, the original coordinate system is relabeled. Also, any number of lines can be drawn through the interior of our cell, intersecting an edge at a point. For instance, for the triangle or 2-D simplex, a line can be drawn from each vertex to a point on its opposite side (edge), this point is then written in terms of the basis of three weighted vectors -- our barycentric-ized vertices:
A change of basis takes place; we zoom in. Barycentric coordinates expand the vertices onto a smaller, more refined scale, adding degrees of freedom, revealing underlying dimensions. As the space grows in complexity, each vertex, boundary and interior point transforms into a linear combination -- weighted by the barycentric coordinates acting as coefficients -- of the newly defined vertices. Essentially, the original coordinate system is relabeled. Also, any number of lines can be drawn through the interior of our cell, intersecting an edge at a point. For instance, for the triangle or 2-D simplex, a line can be drawn from each vertex to a point on its opposite side (edge), this point is then written in terms of the basis of three weighted vectors -- our barycentric-ized vertices:
point = a1v1 + a2v2 + a3v3.
So let each cell of any particular dimension be increasingly refined with lines drawn to points along its edges, further dissecting and contorting its volume, further detailing the enclosed (convex) compacted space. The areas and volumes of faces and simplices of our complex, it should be pointed out, are quantized according to elementary Planck units. Lines of partition [field lines, if you will] intersect at the center of mass -- the source point of the cell. Individual particles of matter and radiation are thus created.For example, an electron can correspond to a factored network of quotient spaces in a fluctuating state, stuck in a loop due to the particular configuration, compressed into a bounded condition. Increasing and decreasing refinement within a certain range corresponds to its everchanging position and momentum. As the space of that cell increases in detail due to fluctuating factoring, a photon is absorbed. As it decreases, a photon is expelled. This represents a probability distribution as a result of, or corresponding to, the quantum partitioning. The electron can be localized by the barycentroid (or multiple barycentroids) of the cell, insensitive to noise and deformations.
Looking at our cell-complex from another perspective, continually varying spatial vortices collectively forming an ever-shifting strange attractor, an emergent phenomenon, manifests in the macro-world as spacetime, the fabric of it, to use a hackneyed mataphor. Piecewise, a strange attractor renders the overall appearance of the cell as it goes through its fluctuations, fractalizing space. A collection of these cells (simplex, node), interfacing at their boundaries (face, surface), on any required dimension, induces neighboring individual -- quantum level -- cells to arrange their interior structures in sympatico, either by means of extensions of partitioning lines from the source point crossing respective boundaries, or through resonation of sub-vortical frequencies.
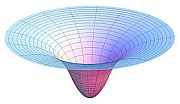 Think of a cone made from a sheet of paper as you twist its pointed-end tighter and tighter. That is the space, or the simplicial complex, of gravity, barycentric coordinates standing for centers of mass [barycenter means center of mass or gravity]. Space, taffy-like, creates the surface appearance of curvature due to its contraction and stretching, to its folding and squeezing. The underlying cause may be attributed to the increasing refinement -- or factoring -- of the sections of simple quotient spaces -- factor groups of denser symmetry -- spontaneously generating, and nested in a hierarchy of sub-domains. Three-dimensionally, we can think of a tetrahedron as homeomorphic to a solid ball, an image that seems to be more agreeable for its natural symbol of centering.
Think of a cone made from a sheet of paper as you twist its pointed-end tighter and tighter. That is the space, or the simplicial complex, of gravity, barycentric coordinates standing for centers of mass [barycenter means center of mass or gravity]. Space, taffy-like, creates the surface appearance of curvature due to its contraction and stretching, to its folding and squeezing. The underlying cause may be attributed to the increasing refinement -- or factoring -- of the sections of simple quotient spaces -- factor groups of denser symmetry -- spontaneously generating, and nested in a hierarchy of sub-domains. Three-dimensionally, we can think of a tetrahedron as homeomorphic to a solid ball, an image that seems to be more agreeable for its natural symbol of centering.
 Onion-skin slices superimposed on one another, interconnected and interrelating, subject to positive amplification and negative feedback constraints. Layers of spacetime embedded within each other -- concentric spheres -- yet separable along an imaginary axis. Viscosity thickening towards the bottom or center, bubbling up new micro-states from nano-moment to nano-moment, evolving fresh pseudo-stable surfaces through some kind of force convection.
Onion-skin slices superimposed on one another, interconnected and interrelating, subject to positive amplification and negative feedback constraints. Layers of spacetime embedded within each other -- concentric spheres -- yet separable along an imaginary axis. Viscosity thickening towards the bottom or center, bubbling up new micro-states from nano-moment to nano-moment, evolving fresh pseudo-stable surfaces through some kind of force convection.
Simple refers to non-divisibility. Each factor group -- each sub-domain of compacted space -- is a whole unto itself, locked in a preferred arrangement or quantized set of arrangements. The mesh size of any specific simplex net varies relatively, but must be no greater than a suitable Planck designation or limit based on the compact nature of the associated Lie group in Hilbert Space. An appropriate distance-metric can be imposed from without but understood only as an artifact for purposes of calculation. Being topological, the underlying field has no inherent metric; in a topological space distance has no meaning. Objects exist in and of themselves without reference to any background coordinate system. Furthermore, thinking of space as a fluid medium allows us to forgo the associated notions of rigidity and flatness of space inherent in our concept of manifold. It bends and twists and can reform into any conceivable topologically valid shape. Time and motion are thus seen as effects of this constant partitioning. Particles as constricted loops, trapped in a web of symmetrically bound energy. Forces as changes in the loop structure due to fluctuation of the spatial components -- the factors.
