f (x,y,c) = 0,
where c is an arbitrary constant, defines a family of curves, one curve of the family is determined by a given value of c. The direction of a curve of the family at any point is given by ∂y/∂x = - ∂f/∂x/∂f/∂y. And the differential equation of the family F(x, y, ∂y/∂x) = 0 gives a relation between a point and a direction of a curve through that point, which is true for any point and any curve of the family.
Now, let's consider a differential equation of the first order in three variables.
The surface equation (1) f (x,y,z,c) = 0 satisfies a differential equation of the form:
(2) P dx + Q dy + R dz = 0,
where P, Q, and R are functions of (x,y,z) but do not involve c.
The reason is that from equation (1) we have
(3) ∂f/∂x dx + ∂f/∂y dy + ∂f/∂z dz = 0,
and the elimination of c from (3) and (1) gives (2).
Geometrically we may say that the coefficients P, Q, R determine a vector
(4) P i + Q j + R k.
at each point of space, and the differentials dx, dy, dz determine a vector(5) dx i + dy j + dz k.
The differential equation (2) asserts that these two vectors are perpendicular to each other. That is, the direction dx:dy:dz is the direction of a tangent to a curve at any point on it [collectively, the direction of the curve] and, at each point, is orthogonal to the direction P:Q:R. Hence the vector (5) is restricted to lie in a plane perpendicular to (4). In other words, the differential equation defines a plane of infinitesimal vectors (5) at each point of space. The totality of these vectors forms what we may call a planar element. The problem of integration is to arrange these planar elements into surfaces. Geometrically, to solve the equation is to determine geometric loci so that the condition of perpendicularity is fulfilled for directions on each locus.
*************
In the integrable case these loci consist of surfaces which are orthogonal at each point to the direction P:Q:R. Then any curve whatever drawn on the surface has the property of perpendicualrity at each of its points.In the nonintgrable case no such family of surfaces exists. We may, however, upon any surface whatever, find a family of curves which has the property of being perpendicular to the direction P:Q:R.
*************
For if F(x,y,z,c) = 0 is any arbitrarily assumed surface, then any direction on the surface satisfies the equation(6) ∂F/∂x dx + ∂F/∂y dy + ∂F/∂z dz = 0.
This equation taken simultaneously with (2) defines a family of curves. These curves necessarily lie on (6).
*************
Now, consider the linear partial differential equation(1) P ∂z/∂x + Q ∂z/∂y - R = 0,
where P, Q, R are functions of x, y, z.
Let (2) z = f(x, y) be a solution of (1). The normal at any point to the surface defined by (2) has a direction dz/dx:dz/dy:-1, and (1) asserts that this direction is orthogonal to P:Q:R. That is, the values of P, Q, and R as determined at any point determine a direction on the surface (2). Hence if this direction is followed from point to point of (2), a curve is traced on (2). The curve is, however, a solution of the equations
(3) dx/P = dy/Q = dz/R.
[An aside: This information is taken from a book on Advanced Calculus of course, I didn't make it up. Notice, if you will, that the notation for the above paragraph and that of the previous exposition are reversed. That is, P, Q, and R, play opposite roles. First, direction cosines normal to the surface, and second, confined to the surface. However, the idea of orthogonality is the same in both; the notation is just the notation, confusing at it may sometimes be.]Hence through every point of (2) there goes a curve of the family defined by (3). These curves are called characteristics, and any solution of (1) is a locus of characteristics. Conversely, any surface that is a locus of characteristics will be a solution of (1), since its normal at each point is perpendicular to a curve of (3) and hence to P:Q:R. The problem of solution is then reduced to grouping the curves (3) into surfaces.
*************
It is important to notice the relation between the equations:(1) P ∂z/∂x + Q ∂z/∂y - R = 0,
(2) dx/P = dy/Q = dz/R,
(3) P dx + Q dy + R dz = 0,
with P, Q, R the same in all equations. Equations (2) represent a family of curves, equation (1) represents surfaces made up of these curves, and equation (3) represents surfaces orthogonal to such curves provided the equation has a solution. Thus, as an example,dx/x = dy/y = dz/z
represents straight lines through the origin,
x ∂z/∂x + y ∂z/∂y = z
represents cones with vertex at the origin, and
x dx + y dy + z dz = 0
represents spheres with center at the origin.
When the family of curves (2) is given, the surfaces (1) always exist, but the surfaces (3) are not always possible.
*************
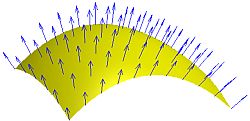Now, having said all that, let's consider the infinitesimal differentials that reside on a particular curved surface as vector components composed of magnitude and direction, the usual vector identity. Let's also consider any sequence of differentials that are strung together continuously, as they traverse the hills and valleys of the surface from point to point, as a curve. And, the collection of all such curves as a family of curves. This family can be said to make up or comprise the surface. It generates and spans the manifold, in other words.The gradient at a given set of coordinates for each dimension of a surface is a vector orthogonal to, or normal to, the surface at that point. Its components are the products of unit vectors, one for each dimension, and the values of partial derivatives of the equation or function describing the surface at that point.
(1) f (x,y,z,c) = 0 [equation of surface in 3-space]
(2) grad (f) = ∂f/∂x i + ∂f/∂y j + ∂f/∂z k,
The entire set of such gradients, one for each point on each curve of the family that comprises the surface, make up, or form, a vector field.
Now, let's make an analogy. Consider the state vector of a particular quantum system expanded in terms of the linear superposition of a specific series of mutually orthogonal bases eigenstates of the operator corresponding to the property of interest:
(3) | PSI > = c1| psi1 > + c2| psi2 > + ... + cn| psin >
where the coefficients of expansion, the c's, are weighted proportionality constants -- probability amplitudes -- the values of which depend on the likely outcome of a particular eigenstate. The contribution that each eigenstate makes is determined by the inner product of the magnitude of the eigenstate's projection amplitude and the arbitrary state vector. As mentioned above, the appropriate choice for this set depends, mostly, on what we wish to measure: total energy, position, velocity, momentum, spin, etcetera of a single or multi-particle system. This set is also determined by the nature of the boundary value problem.A hypersurface is the direct sum of separate surfaces acting as expanded components, each one composed of a family of curves having constant functional value. A specific hypersurface may be conceived as a coordinate space, or Euclidean space, embodying all possible surfaces in the same manner as a wavefunction [state vector] can be conceived as a vector space of all possible eigenstates. The nature of both 'surfaces' and eigenstates is predicated and dependent on the hypersurface and wavefunction, respectively, we are considering.
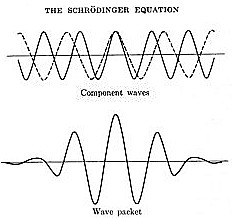
Now, using our infinitesimal differentials [in Hausdorff space] -- dx:dy:dz -- the direction cosines of a curve on our surface, we can form an equivalence between the family of curves on a surface and a set of possible trajectories of a particle, or ensemble of particles, that make up each eigenstate of our wavefunction [in Hilbert space] -- the mixture. The particular equation describing our surface -- a member of the set composing the hypersurface -- would thus correspond to a particular eigenfunction -- a member of the set of components comprising the wavefunction. The wavefunction is expanded in terms of those eigenfunctions [component waves] of interest, each weighted by a coefficient of superposition in the expansion. In the same sense, the specific family of curves composing a specific surface represents only one of many possible alternatives, each rendering a different type of boundary condition. The curves satisfy the equation of the surface as the trajectories can be derived from, or satisfy, the eigenstate, the quantum state that emerges and is expressed when a measurement is taken on the wavefunction.
The above situation is the condition of the time-independent Schrodinger wave equation. It solves for a single monochromatic wave the rays of which can be said to represent the set of particle trajectories when a fixed energy value or frequency is given. The eigenfunction of our single-frequency wave would thus correspond to one surface equation in our analogy. You would thus require an infinite number of such equations to satisfy all posssible monochromatic waves across a range of energies. To arrive at a wavefunction that transcends the constant-energy restriction, we need to increase the order of the equation by forcing time to be dependent -- PSI, a propagating wavefunction in x-y-z-space dependent on time, the coordinate, the point, (x,y,z), a function of time.
The Schrodinger time-dependent equation accomplishes this. Each wavefunction, or wave packet, taken as a superposition of monochromatic plane waves then corresponds to a family of surfaces, each surface comprised of an infinite number of curves as the rays of a plane wave correspond to an infinite number of particle trajectories. Each individual surface that solves the differential equation equals a constant; each particular eigenstate derivable from our wavefunction, composed of an infinite number of possible trajectories, has constant energy or frequency.
It's the difference between a cross-section of a video -- a snapshot or still -- fixed at an arbitrary time and constrained by an operator at a specific energy [space dependent], compared to the entire video of the particle propagating over some time interval, jumping energy levels unpredictably but covering each and every possible quantum state and energy [time dependent].
When we perform a measurement on our wavefunction [apply an operator], one weighted eigenstate emerges on top, so to speak. The relative probabilities of the outcome of the eigenstates being given by the squares of the absolute values of the coefficients of expansion, the modulus squared, the probability density. The gradient as operator manufactures a measurement at a specific point on our surface when that surface represents a specific physical system in a state of potential.
As an example,1 if u(x,y,z,t) represents a temperature function, the surface is an isothermal surface. Let P0 denote a point (x0, y0, z0) interior to a solid body and S a plane or smooth curved surface through P0. At a time t0 the flux F(x0, y0, z0, t0) of heat across S at P0 is the quantity of heat per unit area, per unit time, that is being conducted across S at that point.
Since the direction of the vector
grad (u) = ∂u/∂x i + ∂u/∂y j + ∂u/∂z k,
at P0 on S is that in which u increases most rapidly, the vectorJ = -K grad(u),
where K is the thermal conductivity coefficient of the material, is called the total flux or the current of heat flow at that point. It measures the flux across the isothermal surfaceu(x,y,z,t0) = u(x0, y0, z0, t0) through P0.
Let's zoom out from our picture of interior point residing on surface to that of sphere with center at P0, small enough that all points within and on the sphere are interior to a homogeneous, circumscribed region of a solid body. Furthermore, imagine a field of gradient vectors, orthogonal to the surface of our sphere, but extending in a negative direction -- backwards -- intersecting at the center, the origin of any coordinate system. The gradients represent the uniform radiation of heat, or flux of heat, over a region bounded by the sphere.
Boundary conditions which describe the thermal conditions on the surface of the solid and the initial temperature distribution throughout the solid must accompany the heat equation if we are to determine the temperature function u(x,y,z,t) -- a potential function for the flow of heat. Since P0 can represent any point of the solid body in a domain free from heat sources, the temperature function satisfies the heat equation
ut = k(uxx + uyy + uzz)
where k is the thermal difusivity.
grad (u) = ∂u/∂x i + ∂u/∂y j + ∂u/∂z k,
*************************
1 Example from: Churchill, Ruel, V.; Fourier Series and Boundary Value Problems, 1963.
*************